Research

Early warning signals for bifurcations

A bifurcation marks a sudden qualitative change in a dynamical system as a parameter crosses a threshold–also referred to as a tipping point or a critical transition. They correspond to phenomena such as the onset of an epidemic, a cardiac arrhythmia, and the collapse of an ecosystem. When a system is near to a bifurcation, there are universal properties of bifurcations that can emerge when sufficient data is collected. One example is critical slowing down (shown above), where the recovery rate decreases close to the bifurcation. I am interested in the development of computational tools based on the theory of dynamical systems and machine learning to help predict the onset of a bifurcation in various natural systems.

Relevant work:

Nonlinear dynamics of cardiac arrhythmia

The human heart beats around 100,000 times a day. A healthy heartbeat is the result of electrical propagation that travels through the heart, resulting in contraction of the cardiac tissue and pumping of blood to the body. A cardiac arrhythmia occurs when this propagation is disrupted in some way. Wearable device technology has reached the point where we can monitor the electrical activity of our hearts for extended periods of time, amassing a wealth of data. I am interested in using mathematical models and machine learning to better understand and predict the dynamics of the hearts in patients who have cardiac arrhythmia. This work is in collaboration with cardiologists at the University of British Columbia and Weill Cornell Medicine and experimental physiologists at McGill University.

Relevant work:

Onset of spiral waves in excitable systems

Excitable systems exhibit various types of dynamics. They can be at rest, propagate planar waves following a stimulus (left), propagate self-sustaining spiral waves (right), or show more complicated spatio-temporal behaviour. Spiral waves in the human heart are responsible for ventricular tachycardia—a dangerous cardiac arrhythmia. I am interested in how excitable systems can transition into spiral wave dynamics. To study this, I am combining mathematical models with reinforcement learning—a branch of machine learning designed to discover sequential actions that achieve a pre-defined task.

This work is in collaboration with physiologists in the Bub lab, who are conducting experiments with spiral waves in real cardiac tissue. Videos show motion transients from thin sheets of mouse cardiac tissue.

Mechanistic modelling of biological systems

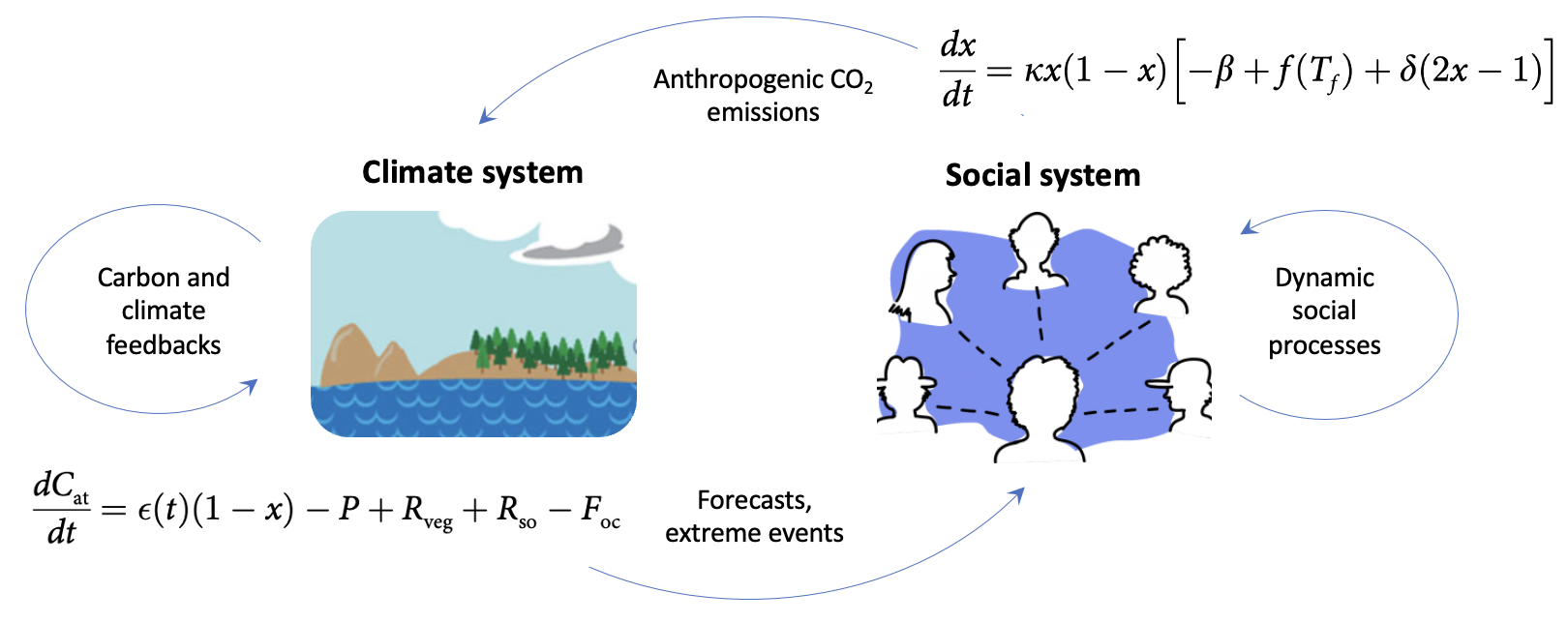
Mathematical models can be built for a biological system based on mechanistic principles. We can then analyse the dynamics of the model (e.g. equilibria, stability, orbits) to gain insights into the biology. I am broadly interested in the application of models to systems in ecology, epidemiology, physiology and Earth System science. A particular aspect I have studied is how human group behaviour interplays with these systems. For example, I extended a simple Earth system model to include dynamics of human behaviour to study how factors such as social norms and rates of social learning affect climate change trajectories.

Relevant work: